问题描述
定义 $f(n,k)$ 表示有多少长度为 $n$ 的排列,使得差的绝对值为 1 的相邻对对数恰好是 $k$。给定 $n$ 求一列,即求 $f(n,*)$。
方法
参考 EI 的《A Story of Small P》的二维生成函数的思想,定义每一段的生成函数如下:
$$ \begin{aligned} f( x,t) & =\sum _{i\geq 1}\sum _{j\geq 1}\left[\text{if} \ i=j=1\ \text{then} \ 1\ \text{else} \ 2\right]\binom{i-1}{j-1}( -1)^{j-1} x^{i} t^{j}\\ & =2\sum _{i\geq 1} x^{i} t\sum _{j'\geq 0}\binom{i-1}{j'}( -t)^{j'} -xt\\ & =\frac{2t}{1-t}\sum _{i\geq 1}( x( 1-t))^{i} -xt\\ & =\frac{tx( 1+x-xt)}{1-x+xt} \end{aligned} $$
解释:想象我们已经有了 $n-1-k$ 个位置不满足相邻相差 1,因此我们把相差 1 的看成一段,总共 $n-k$ 段,考虑容斥,我们钦定一些位置被满足了,其他不满足的位置随意,则 $x^it^j$ 表示的是一个长度为 $i$ 的块,总共 $j$ 段,钦定里面有 $j-1$ 个不满足的位置被满足了,因此有容斥系数 $(-1)^{j-1}$,一共有 $\binom{i-1}{j-1}$ 中钦定的方法。如果一块的大小是 $1$,那么显然分配排列的时候只有一种方法,如果块大小不是 $1$,分配的时候可以从大到小也可以从小到大两种。
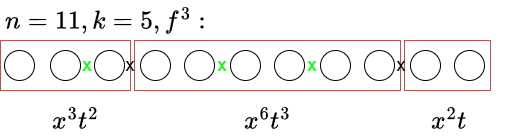
现在用 SEQ 的构造方法,求整个排列的生成函数:$g(x,t)=\sum_{i\ge 1}i!f(x,t)^i$。答案则是 $[x^nt^{n-k}]g(x,t)$(解释:枚举有多少块构成了整个序列,如图,有三块,一共有 $n-k-1$ 个 x,绿色的是钦定的非 x,黑色的 x 表示可有可无,容斥系数 $(-1)^3$)

对 $[x^nt^{n-k}]g(x,t)$ 化简:
$$ \begin{aligned} \text{ans} & =\left[ x^{n}\right]\left[ t^{n-k}\right]\sum _{i=1}^{n} i!f( x,t)^{ \begin{array}{l} i \end{array}} & \\ & =\left[ x^{n}\right]\left[ t^{n-k}\right]\sum _{i=1}^{n} i!( tx)^{i}( 1+( 1-t) x)^{i}( 1-( 1-t) x)^{-i} & ( 2)\\ & =\left[ t^{n-k}\right]\sum _{i=1}^{n} i!t^{i}( 1-t)^{n-i}\left[ x^{n}\right]\left(\frac{x+x^{2}}{1-x}\right)^{i} & ( 3)\\ & =\sum _{i=1}^{n} i!( -1)^{n-i-k}\binom{n-i}{n-i-k}\left[ x^{n}\right]\left(\frac{x+x^{2}}{1-x}\right)^{i} & \\ & =\sum _{i=1}^{n} i!( -1)^{n-i-k}\binom{n-i}{n-i-k} g_{n,i} & \end{aligned} $$
这里需要注意的是 (2)->(3) 的推导,对 $( 1+( 1-t) x)^{i}( 1-( 1-t) x)^{-i}$ 进行展开的时候,需要枚举前后者对 $n$ 次项分别贡献了多少,但我们发现展开后 $(1-t)$ 的次数一定是 $n-i$,只需要关注他的系数。此时发现系数其实就是把 $(1-t)$ 当成 $1$ 然后计算 $\displaystyle\left(\frac{x+x^{2}}{1-x}\right)^{i}$ 的系数。记其 $i$ 次方的 $n$ 次项系数为 $g_{n,i}$。则可以得到最后的式子。
现在的关键是快速计算 $g_{n,i}$。
$$ \begin{bmatrix} \frac{x+x^{2}}{1-x}\left(\frac{x+x^{2}}{1-x}\right)^{2} & ... & \left(\frac{x+x^{2}}{1-x}\right)^{n} \end{bmatrix} =\begin{bmatrix} 1 & & & & & \\ 2 & 1 & & & & \\ 2 & 4 & 1 & & & \\ 2 & 8 & 6 & 1 & & \\ & & & ... & & \\ g_{n,1} & g_{n,2} & & ... & & g_{n,n} \end{bmatrix} $$
观察发现 $\displaystyle \frac{1}{1-x}$ 对一个序列的作用效果是求前缀和,$x+x^2$ 是取前一项和前前一项,因此 $g_{i,j}=Sg_{i-1,j-1}+Sg_{i-2,j-1}$,则:
$$ g_{i,j}-g_{i-1,j}=Sg_{i-1,j-1}+Sg_{i-2,j-1}-(Sg_{i-2,j-1}+Sg_{i-3,j-1})=g_{i-1,j-1}+g_{i-2,j-1} $$
然后设 $g_i(x)$ 表示 $g_{i,1},g_{i,2},...,g_{i,n}$ 的生成函数,则有 $g_i(x)=(1+x)g_{i-1}(x)+xg_{i-2}(x)$。
显然这个递推式可以写为:
$$ \begin{bmatrix} 1+x & x\\ 1 & 0 \end{bmatrix}\begin{bmatrix} g_{i-1}( x)\\ g_{i-2}( x) \end{bmatrix} =\begin{bmatrix} g_{i}( x)\\ g_{i-1}( x) \end{bmatrix} $$
于是可以通过 ntt 合并矩阵计算出 $g_n$ 这一行,然后一次卷积计算出答案的第 $n$ 行。